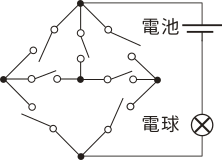
図のような,電池1個,電球1個,スイッチ7個を含む電気回路があります。スイッチのオン・オフの仕方は全部で128通りあり,そのうち電球が点灯するようなスイッチのオン・オフの仕方は全部で\(\boxed{\phantom{hoge}}\)通りあります。
電気が流れない場合の方がイメージしやすかったので全体から引く方針で求めました。
✤下2つが閉じているとき
残り5つのスイッチはどうなっていていも良いので\(2^{5}=32\)通り。
✤下2つが開いているとき
中段の右端と左端に電気が流れなければ電球はつきません。下図のように2パターンが考えられます。\(2^{2}+1=5\)通り。
✤下1つが開いているとき
図のように下の右側が開いていれば,右端に電気が流れなければ電球はつきません。下図のように3パターンが考えられます。\(2^{3}+2^{1}+1=11\)通り。
したがって,電球がつかないのは\(32+5+11 \times 2=59\)通りなので,\(\boxed{\phantom{hoge}}=128-59=69\)通りになります。





