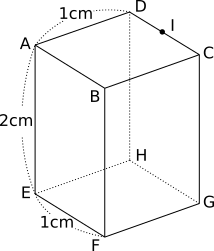
図の直方体ABCD-EFGHについて,辺AD,AE,EFの長さはそれぞれ1cm,2cm,1cmです。また,点Iは辺CDの真ん中の点です。3点A,F,Iを通る平面でこの直方体を切り分けたとき,点Cを含む方の立体の体積は,他方の立体の体積の\(\Box\)倍です。
三角錐を作る方針で簡単に求まりますね。

三角錐K-ABFは三角錐K-CIJの体積の8倍なので,点Cを含む方の立体の体積は,次のように求められます。 \[ 1 \times \frac{1}{2} \div 2 \times 1 \times \frac{1}{3}=\frac{7}{12} ~\rm{cm^{3}} \] ですから,もう一方の立体の体積は次のように求まります。 \[ 1 \times 1 \times 2 - \frac{7}{12} = \frac{17}{12} ~\rm{cm^{3}} \] したがって,答えは\(\displaystyle \frac{7}{12} \div \frac{17}{12} = \frac{7}{17} \)倍と求まります。




