ある立体の展開図は図のようになっています。この立体の体積は\(\Box \rm{{cm}^{3}}\)です。ただし,同じ記号がかかれた辺の長さは等しいとします。
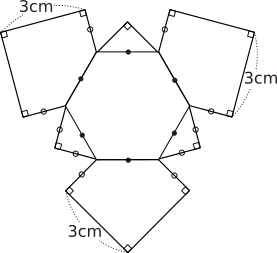
展開図に正六角形があるので切断の仕方はすぐに気が付きますね。

1辺3cm立方体を上の図のように切断したと考えられます。立方体から飛び出した部分は,どれも底辺\(\frac{3}{2}\)cmと高さ\(\frac{3}{2}\)cmの直角二等辺三角形を底面とする,高さ\(\frac{3}{2}\)cmの三角錐です。 \[\frac{3}{2} \times \frac{3}{2} \div 2 \times \frac{3}{2} \times \frac{1}{3} \times (27-3) = \frac{27}{2} \rm{{cm}^{3}}\]




