2024年灘中算数1日目９

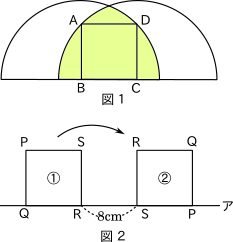
　１辺の長さが８cmである２つの正方形ABCD，PQRSがあります。図１には，点Bを中心とし点Dを通る半円と，点Cを中心とし点Aを通る半円がかかれています。図２のように正方形PQRSが①の位置から②の位置まで直線アの上をすべることなく転がるときに辺PQが通過する部分の面積と，図１の斜線部分の面積の和は\(\boxed{\phantom{hoge}}\rm{{cm}^{2}}\)です。

　辺PQが通過するのは図上段の緑色と赤色の部分です。ピンク色は図１と共通なので２重です。

このことに注意すると，図中段で\(ア+ウ\)と\(イ+ウ\)が作れて，それらは正方形の対角線を半径とする中心角45°の扇形から直角二等辺三角形を引いたものです。ですからこれらは●に移動できます。

図下段では正方形の対角線を半径とする中心角45°の扇形が重なっています。重なり部分■を引く一方で，■の上にある合同な三角形を足すので相殺されます。



以上のことから， \[\left(128 \times \pi \times \frac{1}{4} - 64 \times \pi \times \frac{1}{4}\right)\times 2 + 128 \times \pi \times \frac{1}{8} \times 2 = 200.96\rm{{cm}^{2}}\]